量化混合：一种在最大限度减少模型尺寸的同时将精度影响降到最低的新型量化方法

量化感知训练和推理的统一套件

在多GPU上运行大规模模型可能有助于降低延迟，但会显著增加部署成本，特别是随着模型尺寸的增大。为了缓解这个问题，我们求助于模型压缩技术，并引入了一种新方法，以对精度影响最小的方式对Transformer网络进行量化。我们的技术通过在更少或相同数量的GPU上使用定制的推理核，实现了与FP16模型相似或更好的性能。

我们的方案是灵活的，因为它允许用户尝试任何量化配置，例如用于量化精度的目标位数，以及模型在训练过程中进行量化的调度方式。此外，我们将FP16和量化精度结合起来作为一种混合精度机制，以平滑从高精度到低精度的过渡。最后，我们使用参数的二阶梯度（特征值）来调整训练期间的量化调度。

量化方法

量化主要有两种应用方法：对已训练模型进行离线量化，以及在训练过程中降低数据精度的量化感知训练（QAT）。与前者不同，QAT在训练优化过程中考虑精度损失的影响来训练模型。这将显著提高量化模型的精度。MoQ是在QAT方法的基础上设计的，不同之处在于我们使用混合精度来训练模型以达到目标量化，并定义了降低精度的调度。

所有现有的QAT方法从训练开始到结束都以一定的精度（位数）对模型进行量化。然而，即使使用相对较高的量化精度（8位），模型精度也会有所下降，这对于某些下游任务可能无法接受。例如，Q8BERT尝试对BERT网络进行QAT，这在某些任务上获得了良好的精度，而其他任务（如SQuAD）的F1分数则下降了0.8%。其他技术，例如Q-BERT，在量化参数矩阵时使用大分组大小（128）的分组量化以获得更高的精度，但它们仍然不如基线。

在这里，我们提出MoQ作为一种灵活的线性量化解决方案，允许用户在模型训练时定义调度。类似于迭代剪枝以注入稀疏性，我们从更高的精度（16位量化或FP16）开始量化，并逐渐减少量化位数或FP16部分的混合精度比率，直到达到目标精度（8位）。为了控制精度转换，我们定义了一个超参数，称为量化周期，它指示精度降低何时发生。我们观察到，通过使用这样的调度，我们获得了最接近基线的精度。请注意，为了达到一定的精度，我们需要以一种方式定义起始位数和周期，使得在训练样本数量内，模型最终使用目标位数进行量化。更多信息请参阅量化教程。

为了动态调整量化精度，我们采用特征值作为衡量训练对精度变化敏感度的指标。特征值之前曾被用于（Q-BERT）量化，以选择网络不同部分的精度位数。为了将其与MoQ结合，我们根据特征值的绝对值将其聚类到几个区域，并相应地调整每个区域的量化周期，特征值越大，因子越大，精度降低越慢。

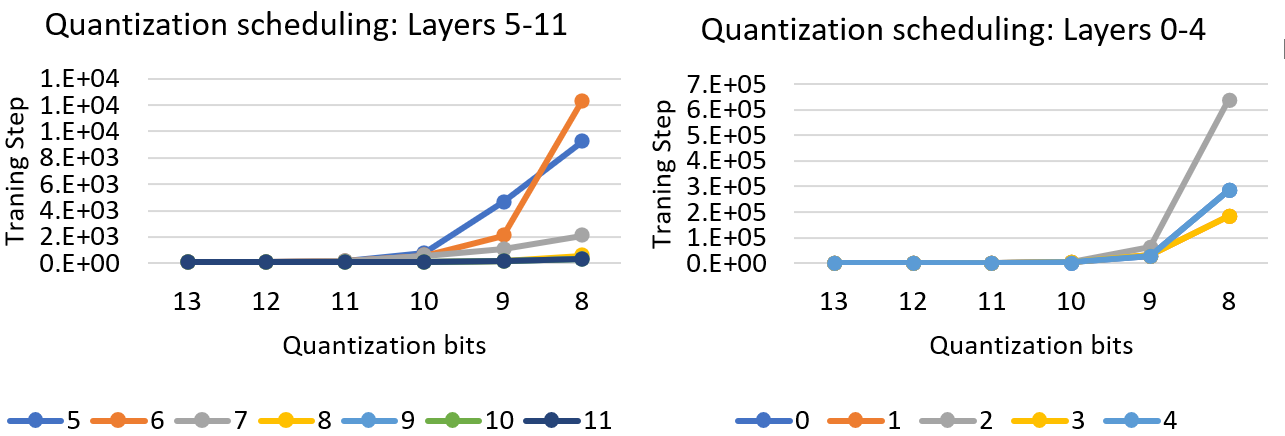
图1. GLUE任务（QNLI）之一的量化调度，使用不同层的特征值。不同颜色显示了Bert-Base的0到11层。

图1显示了将特征值与MoQ结合应用于12层Bert Base模型的结果。正如我们所看到的，前几层（0-4）对降低精度往往比后几层更敏感，因为它们的量化周期比其余层大一个数量级。从该图中观察到的另一点是，相邻层以相同的方式降低精度。例如，图1左侧的第9、10和11层，以及右侧的第0和4层、第1和3层获得了相似的调度。这是由于这些层在整个训练过程中具有相似的特征值。

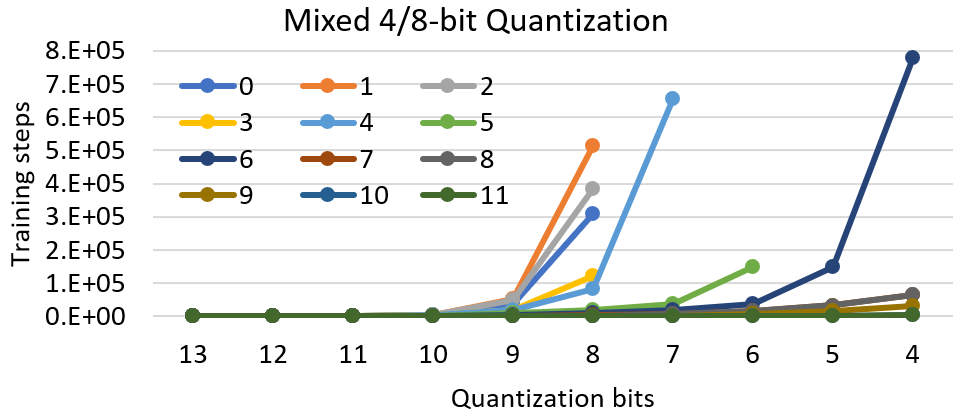图2：QNLI的混合精度量化，目标量化周期为4位。

图2显示了另一种混合精度量化，将目标位数设置为4位，但量化周期通过每层的特征值不断更新。正如我们所看到的，所有层的最终量化位数都不同。由于训练样本不足以减少量化位数，第一层仍然保持8位量化。另一方面，最后几层持续降低精度。我们最终将整个网络的平均精度降低到6位，同时保持了模型的精度（精度下降0.3%）。

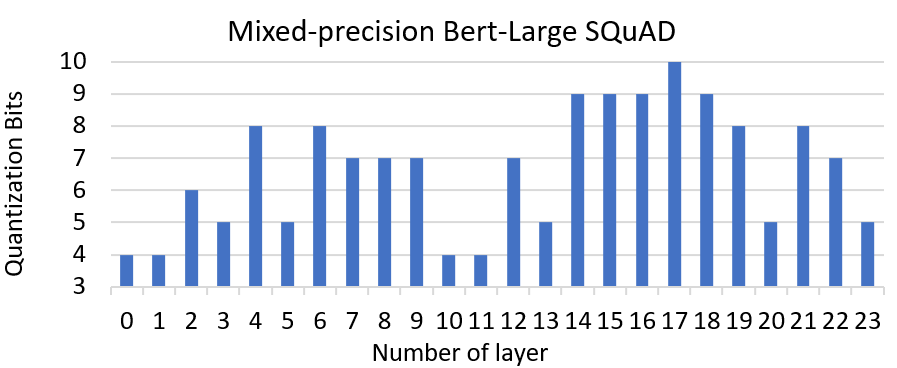图3：使用MoQ对Bert SQuAD plus进行混合精度量化。

另一个例子是，我们使用基于特征值的MoQ对Bert-Large进行SQuAD微调量化。图3显示了在微调结束时每层达到的位数。在这里，与GLUE任务上的BertBase相比，我们看到了略微不同的精度范围。如图所示，我们可以比中间层更激进地降低前几层的精度。此外，最后几层可以容忍非常低的精度，类似于开始层。这种量化方法最终得到了90.56的F1分数，这与基线非常相似。

量化推理核

通过使用其他量化方法，模型量化后，只有在硬件支持整数操作的情况下才能获得性能优势。因此，所有GeMM操作的输入和输出都需要量化。然而，由于输入范围可能因请求而异，在推理时为每个输入找到一个数据范围是具有挑战性的。另一方面，对所有输入使用静态范围可能会影响推理精度。

为了缓解这个问题，我们引入了推理自定义核，它们既不需要硬件支持，也不需要输入量化。这些核读取量化参数并进行即时反量化，并使用GPU核心的浮点单元进行GeMM操作。使用这些核的主要好处是，它们减少了加载模型所需的内存占用，从而我们可以在更少数量的GPU上运行推理，同时通过节省在GPU上运行推理所需的内存带宽来提高性能。

关于量化实现，我们根据数据范围和舍入策略使用不同的算法来量化一个值。我们支持对称和非对称量化这两种最常用的方案。我们对QAT应用了这两种技术，并看到了非常相似的结果，但由于对称方法更简单易于实现，我们的推理核是基于对称方法实现的。关于舍入，我们支持随机舍入作为除普通舍入之外的另一个选项。我们发现，当精度降低到4位或更低时，随机舍入更有帮助，因为它在训练过程中具有无偏的随机行为。

易用性

要通过DeepSpeed启用量化，我们只需通过JSON配置文件传递调度。为了增加量化的影响，我们在参数在优化器中更新之前对其进行量化和反量化。因此，我们不需要在模型侧进行任何更改来量化模型。相反，我们通过降低以FP16格式保存的数据精度来模拟量化影响。通过使用这种实现方式，我们可以完全灵活地根据训练特性（例如步数、参数的特征值和原始FP16数据格式）来改变精度。如这篇博客文章所示，我们可以通过在整个训练过程中自适应地改变量化调度来提高量化模型的质量。有关如何使用MoQ方案的更多信息，请查看我们的量化教程。

提高量化精度。

为了展示我们的量化方案如何保持精度，我们已经在多个任务和网络上实验了MoQ：Bert-Base上的GLUE任务和Bert-Large上的SQuAD。表1显示了未量化的基线（w/o Quant）、训练期间不使用任何调度的基本量化（Basic Quant）以及我们的MoQ方案的精度结果。在不使用任何调度的情况下，8位量化的精度通常不如基线，并且在此工作负载中，精度（ACC）下降了1.02点。相比之下，MoQ使8位量化能够获得与FP16基线相当的精度，甚至略高一点的ACC，这证明了我们量化方法的有效性。

任务	STSB	MRPC	COLA	WNLI	SST2	RTE	QNLI	QQP	MNLI	SQuAD	精度+
无QAT(FP16)	88.71	88.12	56.78	56.34	91.74	65.3	90.96	90.67	84.04	90.56	0
基本QAT	88.9	88.35	52.78	55.3	91.5	64.2	90.92	90.59	84.01	90.39	-0.87
MoQ	88.93	89	59.33	56.34	92.09	67.15	90.63	90.94	84.55	90.71	0.75