DeepSpeed 结合 1 比特 Adam：通信量减少 5 倍，训练速度提升 3.4 倍

2020 年 9 月 8 日

1. 引言

大型模型（如 BERT 和 GPT-3）的可扩展训练需要仔细优化，其基础在于模型设计、架构和系统能力。从系统角度来看，通信已成为主要瓶颈，尤其是在标准 TCP 互连且网络带宽有限的商用系统上。通信压缩是减少此类系统训练时间的重要技术。最有效的通信压缩方法之一是通过误差补偿压缩，即使在 1 比特压缩下，它也能提供稳健的收敛速度。然而，最先进的误差补偿技术仅适用于基本优化器，如随机梯度下降（SGD）和动量 SGD，这些优化器线性依赖于梯度。它们不适用于非线性梯度优化器，如 Adam，后者为许多任务（包括 BERT 类模型的训练）提供了最先进的收敛效率和准确性。对于像 Adam 这样强大的优化器，对梯度的非线性依赖（在方差项中）使得开发基于误差补偿的压缩技术变得具有挑战性，从而限制了最先进通信压缩技术的实际价值。

1.1 背景：经典压缩技术

通信压缩的一种方式是 1 比特压缩，可表示为

$x\to \frac{\|x\|}{\|Sign(x)\|}Sign(x)$

采用这种压缩方式，通过用一个比特表示每个数字，我们可以将内存大小减少 32 倍。问题在于，使用这种直接方法会显著降低收敛速度，这使得该方法无法应用。为了解决这个问题，最近的研究表明，通过使用误差补偿压缩，我们可以在通信压缩的同时获得几乎相同的收敛速度。误差补偿的思想可以概括为：1) 进行压缩，2) 记住压缩误差，然后 3) 在下一次迭代中将压缩误差加回去。对于 SGD，进行误差压缩会导致

$x_t= x_{t-1} - \gamma C(g_t + e_{t-1}), \quad e_t = g_t+e_{t-1}-C(g_t+e_{t-1} )$

其中 C(⋅) 是 1 比特压缩运算符。进行这种误差补偿的好处是，历史压缩误差（e_t 和 e_(t-1)）最终会自行抵消，这可以通过以下方式看出

$x_t=x_{t-1}-\gamma(g_t+e_{t-1}-e_t )$

这种策略已被证明适用于线性依赖于梯度的优化算法，例如 SGD 和动量 SGD。

1.2 将误差补偿应用于 Adam 的挑战

下面我们概述 Adam 算法。其更新规则如下。

$m_{t+1}=\beta_1 m_t+(1-\beta_1 ) g_t$

$v_{t+1}=\beta_2 v_t+(1-\beta_2 ) (g_t )^2$

$x_{t+1}=x_t-\gamma \frac{m_{t+1}}{\sqrt{v_{t+1}} +\eta}$

如上式所示，方差项 v_t 非线性依赖于梯度 g_t。如果我们将基本的误差补偿压缩应用于 Adam，我们会发现 Adam 不会收敛，如图 1 所示。

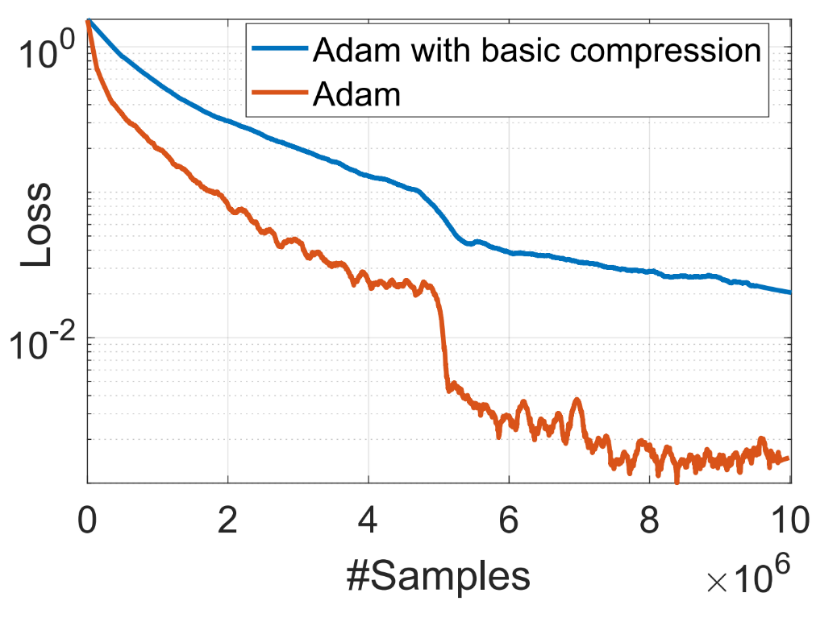
Inapplicability of Error-compensation Compression for Adam due to non-linear dependence on the gradient

图 1：由于对梯度的非线性依赖，误差补偿压缩不适用于 Adam

2. 使用 1 比特 Adam 压缩通信

为了在使用 Adam 优化器的同时压缩通信，我们开发了 1 比特 Adam，它通过预处理解决了梯度中的非线性问题。我们观察到，非线性项（方差 v_t）的变化幅度在训练几个 epoch 后显著减小，之后将 v_t 设为常数不会改变收敛速度。所提出的 1 比特 Adam 优化器，如图 2 所示，由两部分组成：预热阶段，本质上是原始 Adam 算法；以及压缩阶段，该阶段保持方差项不变，并将剩余的线性项（即动量）压缩为 1 比特表示。

算法的压缩阶段由一个阈值参数控制（如图 2 所示）。当我们检测到“方差”的变化低于某个阈值时，我们切换到压缩阶段。我们的研究表明，预热阶段仅需要总训练步骤的 15-20%。

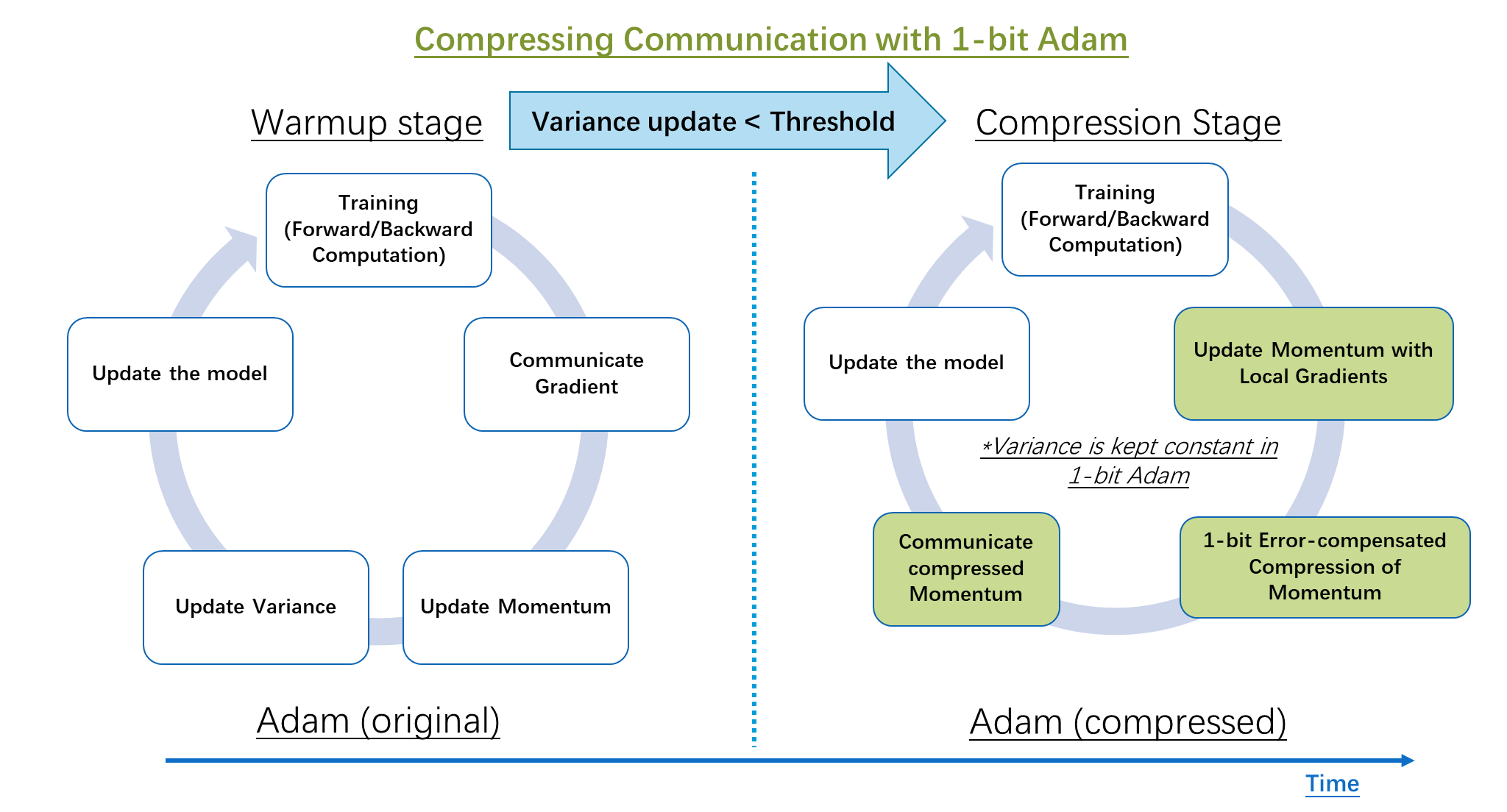
Comparison of distributed training steps in classic Adam and the proposed 1-bit compressed Adam algorithm

图 2：经典 Adam 与所提出的 1 比特压缩 Adam 算法中分布式训练步骤的比较

2.1 1 比特 Adam 的内部工作原理

1 比特 Adam 的权重更新规则由以下方程决定。

对于第 i 个 worker，在压缩阶段

$m_{t+1}^{(i)}=\beta_1 m_t+(1-\beta_1 ) g_t^{(i)}$

$\widehat{m}_{t+1}^{(i)}=C(m_{t+1}^{(i)}+e_t^{(i)}), \quad e_{t+1}^{(i)}=(m_{t+1}^{(i)}+e_t^{(i)} )-\hat{m}_{t+1}^{(i)}$

$m_{t+1}^{(ave)} = \frac{1}{n}\sum_{i=1}^n \hat{m}_{t+1}^{(i)}$

$\hat{m}_{t+1}^{(ave)}=C(m_{t+1}^{(ave)}+e_t^{(ave)} ),\quad e_{t+1}^{(ave)}=(\hat{m}_{t+1}^{(ave)}+e_t^{(ave)} )-\hat{m}_{t+1}^{(ave)}$

$m_{t+1}=\hat{m}_{t+1}^{(ave)}$

$x_{t+1}=x_t-\gamma \frac{m_{t+1}}{\sqrt{v_{warmup}}+\eta}$

其中 x_t 是迭代 (t-1) 后的模型，m_t^(i) 和 e_t^(i) 是迭代 (t-1) 后 worker i 上的动量和压缩误差，v_warmup 是预热阶段后的方差项。

2.2 应对 1 比特 Adam 的系统挑战

除了算法挑战之外，在训练系统中应用 1 比特 Adam 还存在两个系统挑战。首先，我们需要高效的内核将动量转换为 1 比特表示。其次，我们需要高效的通信方案来在不同 GPU 之间交换这种压缩的动量。压缩的目标是减少总训练时间，以便带宽受限互连的商用系统可以用于训练大型模型。我们在 DeepSpeed 中解决了这些挑战，并引入了为通信受限系统训练而完全优化的 1 比特 Adam 实现。

3. 1 比特 Adam 在通信受限系统上的优势

1 比特 Adam 提供了与 Adam 相同的收敛性，通信量减少高达 5 倍，使得 BERT-Large 预训练的吞吐量提高高达 3.5 倍，SQuAD 微调的吞吐量提高高达 2.7 倍。这种端到端吞吐量的提升得益于压缩阶段观察到的 6.6 倍（图 3）和 6.2 倍（图 4）的加速。值得一提的是，我们的 1 比特 Adam 优化器在 40 千兆以太网系统上表现出极佳的可扩展性，其性能与 Adam 在 40 千兆 InfiniBand QDR 系统上的可扩展性相当。我们注意到，根据 iperf 基准测试，40 千兆以太网的有效带宽为 4.1 Gbps，而 InfiniBand 根据 InfiniBand perftest 微基准测试提供了接近峰值 32Gbps 的带宽。

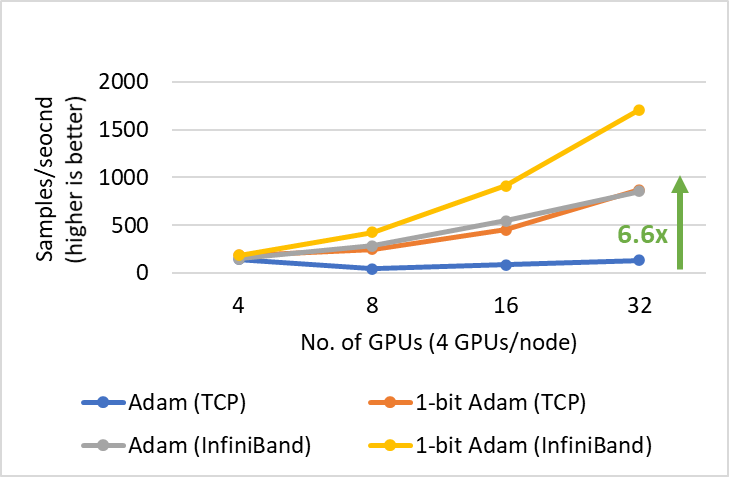
BERT-Large Pretraining

图 3：1 比特 Adam 在 V100 GPU 上进行 BERT-Large 预训练的可扩展性，批处理大小为 16/GPU。

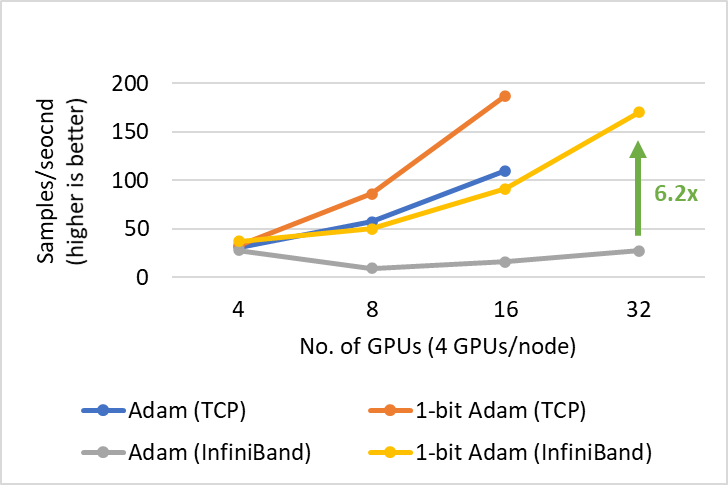
SQuAD Finetuning

图 4：1 比特 Adam 在 V100 GPU 上进行 SQuAD 微调的可扩展性，批处理大小为 3/GPU。

4. 深入了解 1 比特 Adam 评估结果

与 Adam 相同的收敛性

使用 1 比特 Adam 的一个主要问题是收敛速度，我们发现 1 比特 Adam 可以使用与 Adam 相同数量的训练样本实现相同的收敛速度和可比较的测试性能，如图 5 所示。

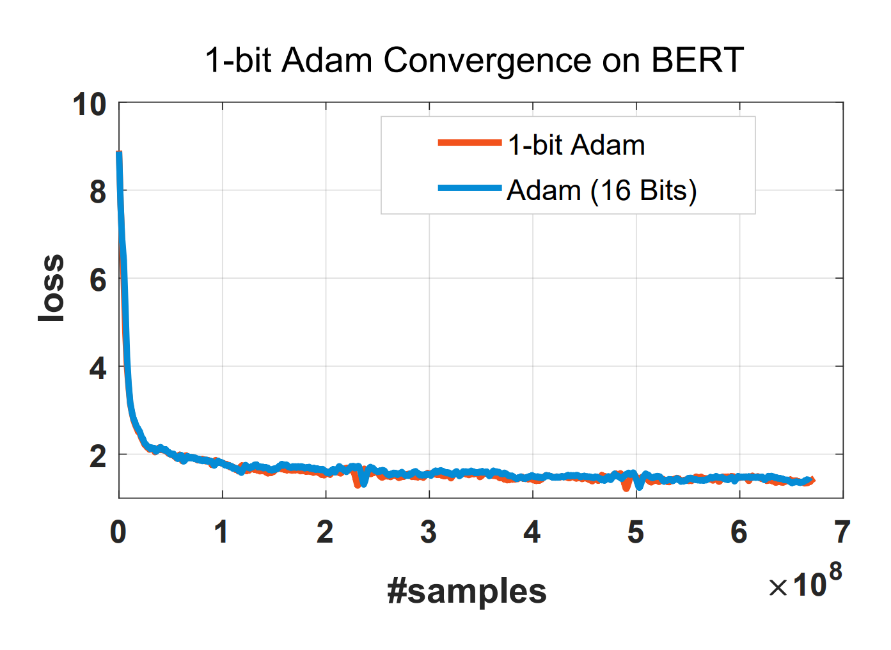
1-bit Adam convergence

图 5：1 比特 Adam 使用相同数量的训练样本与 Adam 一样收敛。

详细的 BERT-Base 和 BERT-Large 结果如表 1 所示。我们看到，在未压缩和压缩情况下，分数都与原始模型相当或更好。

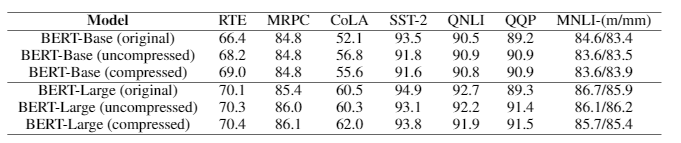
1-bit Adam convergence table

表 1：验证 1 比特 Adam 在各种测试任务上的正确性

通信量减少高达 5 倍：1 比特 Adam 提供了与 Adam 相同的收敛性，并在 16 比特（FP16）训练的压缩阶段将通信量减少了 16 倍。对于 BERT 预训练，由于我们观察到预热阶段仅占端到端训练时间的 15%，这导致总通信量减少了 5 倍。

计算原始 Adam 与 1 比特 Adam 通信量比率的公式如下

1 / (warmup + (1 – warmup)/16)

在预热阶段占 15% 的情况下，原始 Adam 的通信量是 1 比特 Adam 的 5 倍。

1 比特 Adam 训练 BERT-Large 速度提升 3.5 倍

我们展示了在两种不同带宽受限互连系统上训练 BERT-Large 的两个主要结果：1) 40 千兆以太网（图 5）和 2) 40 Gbps InfiniBand QDR（图 6）。在压缩阶段，我们观察到以太网系统上的吞吐量提高了 6.6 倍，InfiniBand 系统上的吞吐量提高了 2 倍，从而实现了端到端加速（包括预热和压缩阶段）分别为 3.5 倍和 2.7 倍。1 比特 Adam 的主要优势来自于通信量的减少——这得益于我们压缩的动量交换——以及我们定制的 allreduce 操作，该操作使用非阻塞 gather 操作，然后进行 allgather 操作来实现高效的 1 比特通信。

值得注意的是，对于 BERT 预训练，也可以使用 LAMB 等优化器而不是 Adam 来增加总批处理大小以减少通信。然而，根据我们的经验，1 比特 Adam 避免了严格的超参数调整，这对于大批量通常更困难。此外，1 比特 Adam 也非常适用于临界批处理大小较小（无法在较大批处理大小下很好地收敛）的工作负载，例如许多微调任务。

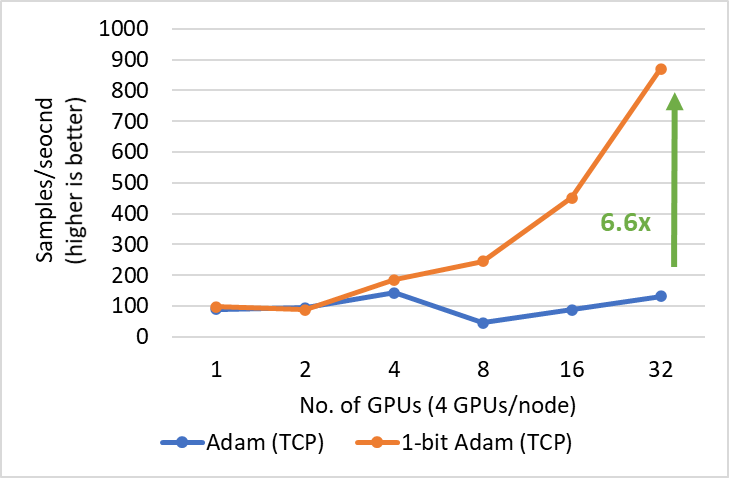
Performance of 1-bit Adam for BERT-Large training on 40 gbps Ethernet

图 5：1 比特 Adam 在 40 Gbps 以太网互连上进行 BERT-Large 训练在压缩阶段的性能。

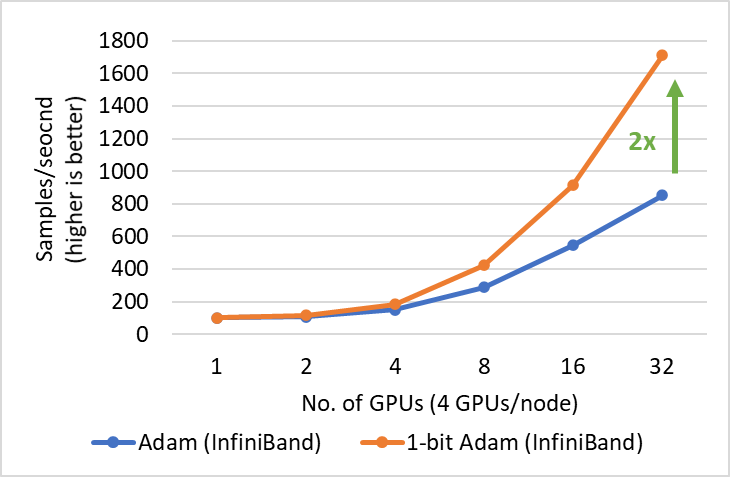
Performance of 1-bit Adam for BERT-Large training on 40 gbps InfiniBand

图 6：1 比特 Adam 在 40 Gbps InfiniBand 互连上进行 BERT-Large 训练在压缩阶段的性能。

1 比特 Adam 对 SQuAD 微调速度提升 2.7 倍

1 比特 Adam 不仅在大规模训练任务上提供了可扩展性，而且在 SQuAD 微调等任务上也表现出色。如图 7 和图 8 所示，1 比特 Adam 在基于以太网和 InfiniBand 的系统上都具有良好的可扩展性，并在基于以太网的系统上提供了高达 6.2 倍的吞吐量提升（在压缩阶段），从而实现了 2.7 倍的端到端加速（25% 预热加 75% 压缩阶段）。对于 SQuAD 微调，我们观察到总批处理大小为 96 时 F1 分数最佳。大于此值的批处理大小会降低收敛速度并需要额外的超参数调整。因此，为了扩展到 32 个 GPU，我们每个 GPU 只能应用 3-4 的小批处理大小。这使得微调任务通信密集且难以扩展。1 比特 Adam 很好地解决了扩展挑战，在不增加批处理大小的情况下实现了 3.4 倍的通信量减少，并带来了 2.7 倍的端到端加速。

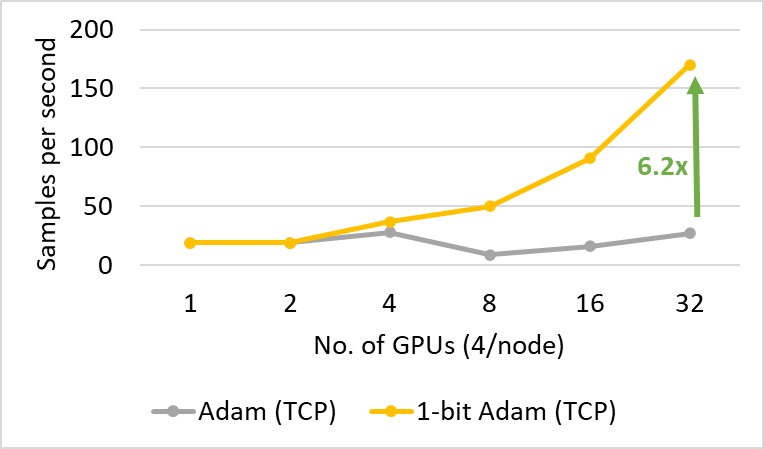
1-bit Adam convergence

图 7：1 比特 Adam 在 40 Gbps 以太网进行 SQuAD 微调在压缩阶段的性能。

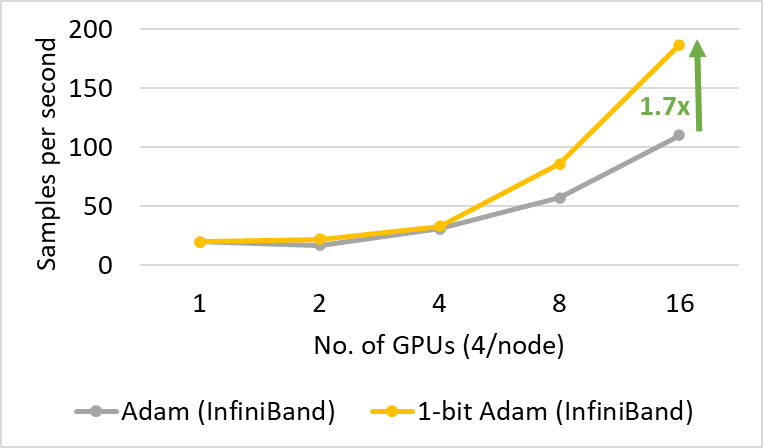
1-bit Adam convergence

图 8：1 比特 Adam 在 40 Gbps InfiniBand 互连进行 SQuAD 微调在压缩阶段的性能。

Twitter Facebook LinkedIn